
Why the Physics Underlying Life is Fundamental and Computation is Not
Our ability to explain gravity fundamentally changed how we interact with our world. So too might an explanatory framework for life transform our future.
Life is undeniably real. It defines the very boundary of our reality because it is what we are. Yet despite this fundamental presence, the nature of life has defied precise scientific explanation. While we recognize “life” colloquially and can characterize its more familiar biological forms, we struggle with frontier questions: how does life emerge from non-life? How can we engineer new forms of life? How might we recognize artificial or alien life? What are the sources of novelty and creativity that underlie biology and technology?
These challenges mirror the limits of our ancestors’ understanding of gravity. They knew objects fell to Earth without understanding why. They observed just a few stars wandering across their night sky and lacked explanations for their motion relative to all the other stars, which remained fixed. It required technological advances — precise mechanical clocks that allowed Tycho Brahe to record planetary motions, Galileo Galilei’s concept of inertial mass, and Isaac Newton’s conception of universal laws — to develop our modern explanation of gravity. While we may be tempted to point to a particular generation that made the conceptual leaps necessary, this transformation took thousands of years of technological and intellectual development before eventually giving rise to theoretical physics as an explanatory framework. The development of physics was based on the premise that reality is comprehensible through abstract descriptions that unify our observations and allow us deeper explanations than our immediate sense perception might otherwise permit.
Our ability to explain gravity fundamentally changed how we interact with our world. With laws of gravitation, we launch satellites, visit distant worlds, and better understand our place in the cosmos. So too might an explanatory framework for life transform our future.
We now sit at an interesting point in history: one in which it is perhaps evident that we have sufficient technology to understand “life,” and according to some we may even have examples of artificial life and intelligence, but we have not yet landed on the conceptual framing and theoretical abstractions that will allow us to see what this means as clearly as we now see gravity. That is, we lack a formal language to talk about life.
Life versus Computation
“Life” has historically been difficult to formalize at this deep level of abstraction because of its complexity. Darwin and his contemporaries were successful in explaining some portion of life because their goal was not to inventory the full complexity of living forms, but merely to explain how it is that one form can change into another, and why this should lead to a diversity of forms, some of them more complex than others. It was not until the advent of the theory of computation roughly 75 years later that it became possible to systematically formalize some notions of complexity (although earlier individual examples of the difficulty of a computation date much earlier). Some thought then, and still think now, that such formalization might be relevant to understanding life. In the historical progression of ideas, proceeding over many many generations, the theory of computation may prove an important step, but not the final or most important one.
The theory of computation, and its derivative concepts of computational complexity, were not explicitly developed to solve the problem of life, nor were they even devised as a formal approach to life or to physical systems. It is important to maintain this distinction because many alive now confuse computation not only with physical reality, but also more specifically with life itself. In human histories, our best languages for describing the frontier of what we understand are often embedded in the technologies of our time; however, the truly fundamental breakthroughs are often those that allow us to see beyond the current technological horizon.
The challenge with “computation” begins with the vast spaces we must consider. In chemical space — defined as the space of all possible molecules — there are an estimated 1060 possible molecules composed of up to 30 atoms using only the elements carbon, oxygen, nitrogen, and sulfur. This is only a very small subset of all molecules we might imagine, and cheminformaticians who study chemical space have never been able to even estimate its full size. We cannot explore all possible states computationally. You may at first think this is solely a limitation of our computers, but in fact it is a limitation on reality itself. Given all available compute time and resources right now on planet Earth, it would not be possible to generate a foundation model for all possible molecules or their functional properties. But even more revealing about the physical barriers is how, if given all available time and resources in the entire universe, it would not be possible to construct every possible molecule either. And, because chemistry makes things like biological forms, which evolve into technological forms, the limitations at the base layer of chemistry indicate that our universe may be fundamentally unable to explore all possible options even in infinite time. The technical term for this is to say that our universe is non-ergodic: it cannot visit all possible states. But even this terminology is not right because it assumes that the state-space exists at all. If nothing inside the universe can generate the full space, in what sense can we say it exists?
A much more physical interpretation, and one that keeps all descriptions internal to the universe they describe, is to assume that things do not exist until the universe generates them. Discussing all possible molecules is just one example, but the idea extends to much more familiar things like technology: even with our most advanced generative models, we could never even imagine all possible technologies, so how could we possibly create them all? This feature of living in a universe that is self-constructing is one clue that reality cannot be computational. The fact that we can imagine possibilities that cannot exist all at once is more telling about us as constructive, creative systems within the universe than it is of a landscape of possibilities “out there” that are all equally real.
This raises deep questions about computational approaches to life, which itself emerges from a backward view of the space of chemistry that the universe can explore; that is, only physical systems that have evolved to be like us can ask such questions about how they came to be. A challenge in the field of chemistry relevant to the issue of defining life is how one can identify molecules with function, that is, ones that have some useful role in sustaining the persistence of a living entity. This is a frontier research area in artificial intelligence-driven chemical design and drug discovery and in questions about biological and machine agency. But function is a post-selected concept. Post-selection is a concept from probability theory, where one conditions the probability space on the occurrence of a given event after the event occurs. “Function” is a concept that can only be defined relative to what already exists and is, therefore, historically contingent.
A key challenge then emerges based on the limits of our models: we can only calculate the size of the space evolution selects functional structures within by imposing tight restrictions on the space of interest (post-selecting) so we can bound the size of the space to one we can compute. It may be that the only sense in which this counterfactual space is “real” is within the confines of our models of it. Chemical space cannot be computed, nor can the full space be experimentally explored, making probability assignments across all molecules not only impossible but unphysical; there will always be structure outside our models which could be a source for novelty. To stress the point here, I am not indicating this as a limitation on our models themselves, but on reality itself and, by extension, on what laws of physics could possibly explain how life emerges from such large combinatorial spaces.
Analogies to the theory of computation do not fit, because computation is fundamentally the wrong paradigm for understanding life. But if we were to use such an analogy, it would be like predicting the output of programs that have not yet been run. We know from the very foundations of the theory of computation that this kind of forward-looking algorithm runs into epistemologically uncertain territory. A prime example is the halting problem, and related proofs that one cannot in general determine whether a given program will terminate and produce an output or run forever. One could make a machine that could describe this situation (what is called an oracle) and solve the halting problem in a specific case, but then the oracle itself would introduce new halting problems. I could assume infinity is real and there will always be a system that can describe another, but even this would run into new issues of uncomputability. New uncomputable things lurk no matter how you patch your system to account for other uncomputable things. Furthermore, infinity is a mathematical concept that itself may not correspond to a physical reality beyond the boundaries of the representational forms of the external world constructed within the physical architecture of human minds and human-derived technologies.
Complexity, in a computational sense of the word, describes the length of the shortest computer program that produces a given output — and it is also generally uncomputable. More important for physics is that it is also not measurable. We might try to approximate complexity with something computable, but this will depend on our choice of language and, therefore, is an observer-dependent quantity and not a good candidate for physical law. If we assume there is a unique shortest program, we must assume infinity is real to do so, and we have again introduced something non-physical. I am advocating that we take the fact that we live in a finite universe with finite resources and finite time seriously, and construct our theories accordingly — particularly in accounting for historical contingency as a fundamental explanation. We need to take seriously our finite, self-constructing universe because this will allow us to embed ideas about life and open-ended creativity into physics, and in turn explain much more about the universe we actually live in. Among the most important aspects of physics is metrology — the science of measurement — because it allows standardization and empirical testing of theory. It also allows us to define what we consider to be “laws of physics” — laws like those underlying gravitation, which we assume to be independent of the observer or measuring device. Every branch of physics developed to date rests on a foundation of abstract representations built from empirical measurement; it is this process that allows us to see beyond the confines of our own minds.
For example, in the foundations of physics, we talk about how laws of physics are invariant to an observer’s frame of reference. Einstein’s work on relativity is exemplary in this regard: when experiments showed the speed of light yielded the same value regardless of the measuring instrument’s motion, Einstein equated the speed of light to a law of physics using the principle of invariance. This principle is important because if something is invariant, it does not depend on what the observer is doing; they will always measure it the same way. Einstein’s peers were not willing to take the measurement at face value. Many assumed the conception that the speed of light could change with the observer was correct, consistent with other sense perceptions of the world, and therefore that the measurements must be wrong. They assumed something must be missing from the physical measurements, like the presence of an ether (a substance hypothesized to fill space to explain the data). Indeed, they were missing something physical, but it was because they assumed their current abstractions were correct, and did not take the measurement seriously enough to change their ideas of what was physically real. The invariance of the speed of light had critically important consequences because following this idea to its logical conclusion (what Einstein did in developing special relativity) indicates that simultaneity (the measuring of events happening at the same “time”) and space are relative, and these insights have subsequently been confirmed by other experiments and observations. This example highlights two important features of physical laws: they are grounded in measurement (confirming they exist beyond how our minds label the world) and they are invariant with respect to measurement.
Assembly Theory and the Physics of Life
As an explanation for the physics underlying what we call “life,” my colleagues and I are developing a new approach called assembly theory. Assembly theory as a theory of physics is built on the idea that time is fundamental (you might call it causation) and as a consequence historical contingency is a real physical feature of our universe. The past is deterministic, but the future is undetermined until it happens simply because the universe has yet to construct itself into the future (and the possibility space is so big it cannot exist until it happens). This may seem a radical step, so how did we get here from thinking about life?
We started with the question of how one might measure the emergence of complex molecules from unconstrained chemical systems. The question was easy to state: how complex does something need to be such that we might say only a living thing can produce it? We were interested in this because we work on the problem of understanding how life arises from non-life, and this requires some way of quantifying the transition from abiotic to living systems. This led to the development of a complexity measure, the assembly index, which my colleague Lee Cronin at the University of Glasgow originally developed from thought experiments on the measurement and physical structure of molecules.
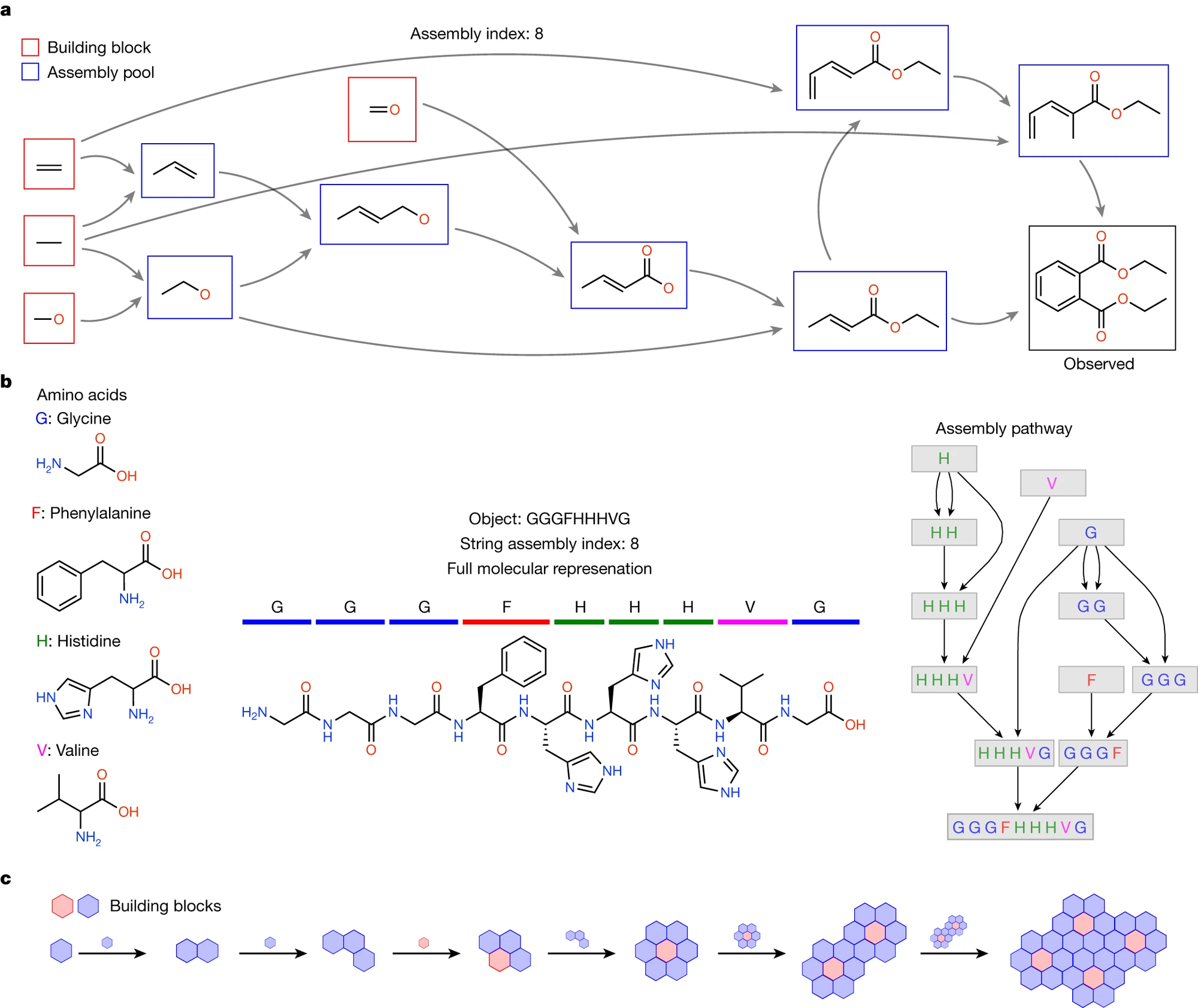
The idea is startlingly simple. The assembly index is formalized as the minimum number of steps to make an object, starting from elementary building blocks, and reusing already assembled parts. For molecules, these parts and operations are chemical bonds. This point on bonds is important: assembly theory uses as its natural language the physical constraints intrinsic to the objects it describes, which can be probed by another system, such as a measuring device. However, we also regard that any mathematical language we use to describe the physical world is not the physical world. What we are looking for is a language that at least allows us to capture the invariant properties of the objects under study, because we are after a law of physics that describes life. We consider the assembly index to represent the minimum causation required to form the object, and this is, in fact, independent of how we label the specific minimum steps. Instead, what it captures is that there is a minimum number of ordered structures necessary for the given structure to come to exist. What the assembly index captures is that causation is a real physical property, automatically implying there is an ordering to what can exist, and that objects are formed in a historically contingent path. This raises the possibility that we may be able to measure the physical complexity of a system, even if it is not possible to compute it.
Assembly theory’s two observables — assembly index and copy number — provide a generalized quantification of the selective causation necessary to produce an observed configuration of objects. Copy number is countable; it is how many of a given object you observe. Our conjecture is that there is a threshold for life, because objects with high assembly indices do not form in high (detectable) numbers of copies in the absence of life and selective processes. This has been confirmed by experimental tests of assembly theory for molecular life detection. If we return to the idea of the vastness of chemical space, we can see why this idea is important. If the physics of our universe operated by exhaustive search, we would not exist because there are simply too many possible configurations of matter. What the physics of life indicates is the existence of historically contingent trajectories, where structures made in the past can be used to further elaborate into the space of more complex objects. Assembly theory suggests a phase transition between non-life (breadth-based search of physical structures) and life (depth-first search of physical structures), where the latter is possible because structures the universe has already generated can be used again. Underlying this is an absolute causal structure where complex objects reside, which we call the assembly space. If one assumes everything is possible, and the universe can really do it all, you will entirely miss the structure underlying life and what really gets to exist, and why.
Determined Pasts, Non-Determinable Futures
An important distinction emerges from the physics of life: you cannot compute the future, but you can compute the past. Assembly theory works precisely because it starts from observed objects and allows reconstructing an invariant, minimum causal ordering for how hard it is for the universe to generate that object through its measurement. This allows us to talk about complexity related to life in an objective way that we expect — if the theory passes the trial and fire of scientific consensus — will play a role like other invariant quantities in physics. This fundamentally differs from computational approaches that depend on the “machine” (or observer), and it builds on the one unique thing theoretical physics has been able to offer the world: the ability to build abstractions that reach deeper than how our brains label data to describe the world.
By taking measurement in science seriously and recognizing how our theories of physics are built from measurement, assembly theory offers a lens through which we might finally understand life as fundamental — not as a computation to be simulated but as a physical reality to be measured. In this view, life is not merely a special case of computation but something more fundamental: a physical reality that can be measured, quantified, and understood through invariant physical laws rather than observer-dependent computations. This leads to the startling realization that one of the most important features of life is that it produces a set of future states that are not computable, even in principle. This means a paradigm for accurately understanding intelligence, consciousness, and decision making is intrinsically missing in our current science that takes as its foundation the idea that everything can happen and everything can be modeled. This does not mean that life will never be understandable as a purely physical process; it simply points to the fact we are missing the required fundamental physics to be able to explain life in a universe that has a future horizon that is inherently undetermined.
The application of assembly theory in physics introduces contingency at a fundamental level, explaining how the past structures some of the future but not all of it. Life takes inert matter that is predictable and turns it into matter that is unpredictable because of the vast number of possibilities in the phenomenon of evolution, revealing selection as a kind of force that is responsible for the production of complexity in the universe. Life, not computation, unlocks our non-deterministic future. Only by looking beyond our current technological moment to the next technologies creating new life forms will we be able to understand what our future could hold.
Acknowledgments
Many of the ideas discussed herein come from collaborative work with Leroy Cronin.
Notes
1. Figure and caption reproduced from Sharma, A., Czégel, D., Lachmann, M. et al. Assembly theory explains and quantifies selection and evolution. Nature 622, 321–328 (02023) under a CC BY 4.0 license. https://doi.org/10.1038/s41586-023-06600-9 .
—
Sara Imari Walker is the author of Life As No One Knows It: The Physics of Life’s Emergence (Riverhead Books, 02024) and will be speaking at Long Now on April 1, 02025.
Join our newsletter for the latest in long-term thinking
Subscribe